Zystkmt

Die logarithmische Normalverteilung (kurz Log-Normalverteilung) ist eine kontinuierliche Wahrscheinlichkeitsverteilung über der Menge der positiven reellen Zahlen. Sie beschreibt die Verteilung einer Zufallsvariablen X{displaystyle X}, wenn die transformierte Zufallsvariable Y=ln⁡(X){displaystyle Y=ln(X)} normalverteilt ist.

Im Gegensatz zu einer normalverteilten Zufallsvariablen, die nach dem zentralen Grenzwertsatz als Summe vieler verschiedener Zufallsvariablen aufgefasst werden kann, entsteht eine logarithmisch normalverteilte Zufallsvariable durch das Produkt vieler positiver Zufallsvariablen. Somit ist die logarithmische Normalverteilung die einfachste Verteilungsart für multiplikative Modelle.

Definition |

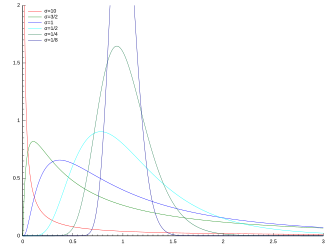
Dichtefunktion der Log-Normalverteilung (mit μ=0{displaystyle mu =0})

Dichtefunktion |

Eine stetige nichtnegative Zufallsvariable X{displaystyle X} unterliegt einer logarithmischen Normalverteilung LN(μ,σ2){displaystyle {mathcal {LN}}(mu ,sigma ^{2})} mit den Parametern μ∈R{displaystyle mu in mathbb {R} } und σ∈R,σ>0{displaystyle sigma in mathbb {R} ,sigma >0}, wenn die transformierte Zufallsvariable Y=ln⁡(X){displaystyle Y=ln(X)} einer Normalverteilung N(μ,σ2){displaystyle {mathcal {N}}(mu ,sigma ^{2})} folgt. Ihre Dichtefunktion ist dann

f(x)=12πσxexp⁡(−(ln⁡(x)−μ)22σ2),x>0{displaystyle f(x)={frac {1}{{sqrt {2pi }}sigma x}},exp {Big (}-{frac {(ln(x)-mu )^{2}}{2sigma ^{2}}}{Big )}quad ,x>0}.

Zweidimensionale Log-Normalverteilung |

Sind X{displaystyle X} und Y{displaystyle Y} zwei log-normalverteilte Zufallsvariablen, dann ist
mit dem transformierten Korrelationskoeffizienten

ρ=exp⁡(ρNσxσy)−1(exp⁡(σx2)−1)(exp⁡(σy2)−1){displaystyle rho ={frac {operatorname {exp} left(rho _{N}sigma _{x}sigma _{y}right)-1}{sqrt {(operatorname {exp} left(sigma _{x}^{2}right)-1)(operatorname {exp} left(sigma _{y}^{2}right)-1)}}}}

deren gemeinsame Wahrscheinlichkeitsdichte definiert als

f(x,y)=exp⁡(−12(1−ρ2)((ln⁡(x)−μxσx)2−2ρln⁡(x)−μxσxln⁡(y)−μyσy+(ln⁡(y)−μyσy)2))2πxyσxσy1−ρ2{displaystyle f(x,y)={frac {operatorname {exp} left(-{frac {1}{2(1-rho ^{2})}}{Big (}{Big (}{frac {ln(x)-mu _{x}}{sigma _{x}}}{Big )}^{2}-2rho {frac {ln(x)-mu _{x}}{sigma _{x}}}{frac {ln(y)-mu _{y}}{sigma _{y}}}+{Big (}{frac {ln(y)-mu _{y}}{sigma _{y}}}{Big )}^{2}{Big )}right)}{2pi xysigma _{x}sigma _{y}{sqrt {1-rho ^{2}}}}}}.

Verteilungsfunktion |

Verteilungsfunktion der Log-Normalverteilung (mit μ=0{displaystyle mu =0})

Damit hat die logarithmische Normalverteilung für x≥0{displaystyle xgeq 0} die Verteilungsfunktion

F(x)=12πσ∫0x1te−(ln⁡(t)−μ)22σ2dt=Φ(ln⁡(x)−μσ){displaystyle F(x)={frac {1}{{sqrt {2pi }}sigma }}int limits _{0}^{x}{frac {1}{t}}mathrm {e} ^{displaystyle -{frac {(ln(t)-mu )^{2}}{2sigma ^{2}}}}mathrm {d} t=Phi left({frac {ln(x)-mu }{sigma }}right)},

wobei Φ{displaystyle Phi } die Verteilungsfunktion der Standardnormalverteilung bezeichnet.

Die Verteilungsfunktion der logarithmischen Normalverteilung erscheint auf doppelt logarithmisch geteiltem Wahrscheinlichkeitspapier als Gerade.

Eigenschaften |

Logarithmus |

Der natürliche Logarithmus von X{displaystyle X} ist normalverteilt, denn

P(ln⁡X≤y)=P(X≤ey)=∫0eyfX(t)dt=∫0ey1tσ2πe−(ln⁡t−μ)22σ2dt={displaystyle P(ln Xleq y)=P(Xleq e^{y})=int _{0}^{e^{y}}f_{X}(t){rm {d}}t=int _{0}^{e^{y}}{frac {1}{tsigma {sqrt {2pi }}}},e^{-{frac {(ln t-mu )^{2}}{2sigma ^{2}}}}{rm {d}}t=}

=∫−∞y1σ2πe−(z−μ)22σ2dz=Φ(y−μσ){displaystyle =int _{-infty }^{y}{frac {1}{sigma {sqrt {2pi }}}},e^{-{frac {(z-mu )^{2}}{2sigma ^{2}}}}{rm {d}}z=Phi left({frac {y-mu }{sigma }}right)}

mit der Verteilungsfunktion Φ{displaystyle Phi } der Standardnormalverteilung.

Maximum |

Die Wahrscheinlichkeitsdichte nimmt ihren maximalen Wert

fmax=12πσeσ2/2−μ{displaystyle f_{text{max}}={frac {1}{{sqrt {2pi }}sigma }},mathrm {e} ^{sigma ^{2}/2-mu }}

an der Stelle x=eμ−σ2{displaystyle x=mathrm {e} ^{mu -sigma ^{2}}} an.

Erwartungswert |

Der Erwartungswert der logarithmischen Normalverteilung beträgt

E⁡(X)=12πσ∫0+∞xe−(ln⁡x−μ)22σ2xdx=eμ+σ22{displaystyle operatorname {E} (X)={frac {1}{{sqrt {2pi }}sigma }}int limits _{0}^{+infty }x;{frac {mathrm {e} ^{-{frac {(ln {x}-mu )^{2}}{2sigma ^{2}}}}}{x}};mathrm {d} x=mathrm {e} ^{mu +{frac {sigma ^{2}}{2}}}}

Varianz |

Die Varianz ergibt sich analog zu

Var⁡(X)=1σ2π∫0+∞(x−eμ+σ22)2e−(ln⁡x−μ)22σ2xdx=e2μ+σ2(eσ2−1){displaystyle operatorname {Var} (X)={frac {1}{sigma {sqrt {2pi }}}}int limits _{0}^{+infty }(x-mathrm {e} ^{mu +{frac {sigma ^{2}}{2}}})^{2};{frac {mathrm {e} ^{-{frac {(ln {x}-mu )^{2}}{2sigma ^{2}}}}}{x}};mathrm {d} x=mathrm {e} ^{2mu +sigma ^{2}}(mathrm {e} ^{sigma ^{2}}-1)} .

Standardabweichung |

Für die Standardabweichung ergibt sich

Var⁡(X)=e2μ+σ2(eσ2−1)=eμ+σ22⋅eσ2−1{displaystyle {sqrt {operatorname {Var} (X)}}={sqrt {mathrm {e} ^{2mu +sigma ^{2}}(mathrm {e} ^{sigma ^{2}}-1)}}=mathrm {e} ^{mu +{frac {sigma ^{2}}{2}}}cdot {sqrt {mathrm {e} ^{sigma ^{2}}-1}}}.

Variationskoeffizient |

Aus Erwartungswert und Varianz erhält man unmittelbar den Variationskoeffizienten

VarK⁡(X)=eσ2−1{displaystyle operatorname {VarK} (X)={sqrt {mathrm {e} ^{sigma ^{2}}-1}}}.

Schiefe |

Die Schiefe ergibt sich zu

γm=(eσ2+2)eσ2−1>0{displaystyle gamma _{m}=(mathrm {e} ^{sigma ^{2}}+2){sqrt {mathrm {e} ^{sigma ^{2}}-1}}>0},

d. h., die Log-Normalverteilung ist rechtsschief.

Quantile |

Ist u(p){displaystyle u_{(p)}} das p-Quantil einer Standardnormalverteilung (d. h. Φ(u(p))=p{displaystyle Phi (u_{(p)})=p}, wobei Φ{displaystyle Phi } die Verteilungsfunktion der Standardnormalverteilung sei),
so ist das p-Quantil der Logarithmischen Normalverteilung gegeben durch

x(p)=eμ+u(p)⋅σ{displaystyle x_{(p)}=mathrm {e} ^{mu +u_{(p)}cdot sigma }}.

Insbesondere ist der Median, d. h. der Wert, bei dem die Verteilungsfunktion den Wert 0,5 annimmt, gegeben durch

x(0,5)=eμ{displaystyle x_{(0,5)}=mathrm {e} ^{mu }}.

Je größer die Differenz zwischen Erwartungswert und Median, desto ausgeprägter ist i.a. die Schiefe einer Verteilung. Hier unterscheiden sich diese Parameter um den Faktor eσ22{displaystyle mathrm {e} ^{frac {sigma ^{2}}{2}}}. Die Wahrscheinlichkeit für extrem große Ausprägungen ist also bei der Log-Normalverteilung hoch.

Charakteristische Funktion |

Die charakteristische Funktion ist für die logarithmische Normalverteilung nicht explizit darstellbar.

Momente |

Für die logarithmische Normalverteilung existieren alle Momente und es gilt:

E⁡(Xn)=enμ+n2σ22{displaystyle operatorname {E} (X^{n})=mathrm {e} ^{nmu +{frac {n^{2}sigma ^{2}}{2}}}}.

Momenterzeugende Funktion |

Die momenterzeugende Funktion existiert nicht für die logarithmische Normalverteilung.

Entropie |

Die Entropie der logarithmischen Normalverteilung (ausgedrückt in nats) beträgt

μ+12ln⁡(2πeσ2){displaystyle mu +{frac {1}{2}}ln left(2pi mathrm {e} sigma ^{2}right)}.

Beziehungen zu anderen Verteilungen |

Beziehung zur Normalverteilung |

Der Logarithmus einer logarithmisch-normalverteilten Zufallsvariablen ist normalverteilt. Genauer:
Ist Y{displaystyle Y} eine N(μ,σ2){displaystyle {mathcal {N}}(mu ,sigma ^{2})}-verteilte reelle Zufallsvariable (d. h. normalverteilt mit Erwartungswert μ{displaystyle mu } und Varianz σ2{displaystyle sigma ^{2}}), so ist die Zufallsvariable X=eY{displaystyle X=mathrm {e} ^{Y}} log-normalverteilt mit diesen Parametern μ{displaystyle mu } und σ2{displaystyle sigma ^{2}}, allerdings bilden diese Parameter nicht Erwartungswert und Varianz von X{displaystyle X}.
Ist ein bestimmter Erwartungswert und eine bestimmte Varianz gewünscht, so kann man dies leicht durch die folgenden Formeln erreichen:

σ2=ln⁡(VarE2+1){displaystyle sigma ^{2}=ln left({frac {operatorname {Var} }{E^{2}}}+1right)} und

μ=ln⁡(E)−σ22{displaystyle mu =ln(E)-{frac {sigma ^{2}}{2}}} oder direkt μ=ln⁡(E2 1Var+E2){displaystyle mu =ln left(E^{2} {sqrt[{}]{frac {1}{operatorname {Var} +E^{2}}}}right)}

Verteilung mit schweren Rändern |

Die Verteilung gehört zu den Verteilungen mit schweren Rändern.

Anwendungen |

Black-Scholes-Modell |

Im Black-Scholes-Modell folgen Aktienkurse einer geometrischen brownschen Bewegung und sind damit logarithmisch normalverteilt. In diesem Modell lassen sich explizit Preise von Finanzoptionen bestimmen.

Einkommensverteilung |

Häufig sind Einkommen log-normalverteilt. Ein Grund ist, dass es relativ wenig bestbezahlte Stellen gegenüber sehr vielen Arbeitsstellen mit eher geringem Einkommen gibt, wobei besonders niedrige Einkommen wieder seltener werden. Das entspricht genau dem Verlauf der meisten Log-Normalverteilungen. Dieser Umstand kann in jedem operativ funktionierenden Unternehmen überprüft werden.

Schätzung von Umsatzziffern von Unternehmen |

Die Logarithmen aller Fakturenbeträge eines Unternehmens folgen annähernd einer Normalverteilung. Der Abstand zwischen dem Logarithmus des kleinsten und dem Logarithmus des größten Fakturenbetrages repräsentiert annähernd die 6-fache Standardabweichung der Normalverteilung der Logarithmen. Dadurch ist es möglich, auf den Mittelwert oder Erwartungswert der Fakturenbeträge (s. o.) der Log-Normalverteilung zu schließen. Multiplikation dieses Mittelwertes mit der Anzahl der gültigen Fakturen ergibt in den meisten Fällen einen akzeptablen Schätzwert für die Größenordnung des Umsatzes eines Unternehmens; wertmäßig liegt er tendenziell zu hoch: Da für solche Schätzungen häufig auch das benfordsche Gesetz gelten sollte, sollte in diesen Fällen auch die Benford-Verteilung zu Rate gezogen werden. Dabei ist zu beachten, dass die Größenordnungen (Stellenwerte) der Rechnungsbeträge nicht gleichverteilt, sondern annähernd normalverteilt sind.

Versicherungsmathematik |

In der Versicherungsmathematik wird die Verteilung der Schadensanzahl häufig mit Hilfe von Zufallsvariablen modelliert, die der Poisson-Verteilung oder der Negativ-Binomialverteilung genügen. Dagegen eignen sich zur Modellierung der Schadenshöhe insbesondere die Gammaverteilung, die Log-Gammaverteilung oder die Log-Normalverteilung.

Die logarithmische Normalverteilung wird wegen der oben besprochenen Schiefe und der damit verbundenen Großschadenneigung bei der Modellierung von Risiken häufig als Verteilung der Schadenshöhe eingesetzt. Sind der Erwartungswert E und die Standardabweichung stdev vorgegeben, so erhält man die Parameter der logarithmischen Normalverteilung wie folgt:

σ=ln⁡(1+(stdevE)2){displaystyle sigma ={sqrt {ln left(1+left({frac {rm {stdev}}{rm {E}}}right)^{2}right)}}}

und

μ=ln⁡E−12ln⁡(1+(stdevE)2){displaystyle mu =ln {rm {E}}-{frac {1}{2}}ln left(1+left({frac {rm {stdev}}{rm {E}}}right)^{2}right)}.

Literatur |

• Eckhard Limpert, Werner Stahel, Markus Abbt: Lognormal distributions across the sciences: keys and clues. In: BioScience. Band 51, Nr. 5, 2001, S. 341–352, doi:10.1641/0006-3568(2001)051[0341:LNDATS]2.0.CO;2 (PDF).